Compiler 구현 사고방식: 계산기
계산기는 수식을 인식할 수 있으므로 이를 기능이 단순한 컴파일러로 볼 수 있다. 계산기 구현을 통해 컴파일러의 구현 사고 방식을 분석해볼 수 있다.
설계할 목표 계산기의 주요 기능 파라미터는 다음과 같다.
- 피연산자: 정수와 소수 지원
- 연산자: 덧셈, 뺄셈, 곱셈, 나눗셈의 사칙연산 및 지수 연산 지원
- 괄호: 소괄호 지원
위의 계산기를 구현하려면 일반적으로 다음의 기본 단계를 거쳐야한다.
- 어휘 분석: 수식 내의 피연산자, 연산자 및 괄호를 스캔하여 토큰 스트림 생성
- 구문 분석: 연산자의 우선순위, 결합 법칙 등의 규칙에 따라 토큰을 조직하여 구문 분석 트리 구축
- 해석 실행: 구문 분석 트리에 따라 연산 결과 계산
어휘 분석: 피연산자와 연산자 식별
수석 123+456 을 예로 들면 어휘 분석 과정에서 순서대로 피연산자 123, 연산자 +, 피연산자 456을 식별해야하며 이를 토큰 스트림 <NUM(123)><ADD><NUM(456)> 으로 변환해야한다. 알고리즘1은 토큰 식별의 사고 방식을 설명한다. 핵심 버퍼 num을 사용하여 현재 읽어야할 피연산자 자릿수를 기록하는 것이다. 이 단계에서는 수식의 합법성 문제(예: 123+456)는 잠시 고려하지 않으며 "-"가 음수 부호인지 뺄셈 부호인지도 구분하지 않는다.
[알고리즘1: 수식에서 피연산자와 연산자 식별]
- 입력: 문자 스트림
- 출력: 토큰 스트림
procedure TOKENIZE(charStream)
let toks, num = ∅
while true do
let cur = charStream.next();
match cur :
case '0'-'9' ⇒ num.append(cur); // num이 비어있으면 맨 앞에 삽입
case '+' ⇒ toks.add(num); toks.add(ADD); num.clear(); // num이 비어있으면 add(num) 무시
case '-' ⇒ toks.add(num); toks.add(SUB); num.clear();
case '*' ⇒ toks.add(num); toks.add(MUL); num.clear();
case '/' ⇒ toks.add(num); toks.add(DIV); num.clear();
case '^' ⇒ toks.add(num); toks.add(POW); num.clear();
case '(' ⇒ toks.add(num); toks.add(LPAR); num.clear();
case ')' ⇒ toks.add(num); toks.add(RPAR); num.clear();
case _ ⇒ break; // EOF 또는 잘못된 문자
end match
end while
end procedure
구문 분석: 연산자 우선순위 파싱 알고리즘
수식 파싱 문제는 매우 고전적이다. 우리가 일반적으로 사용하는 수식 표현 형식은 중위(infix) 표기법이므로 파싱 시, 반드시 연산자의 우선순위와 결합성 규칙을 따라야한다.
- 우선순위(precedence): 지수 연산자 > 곱셈나눗셈 연산자 > 덧셈뺄셈 연산자
- 결합성(associativity): 덧셈, 뺄셈, 곱셈, 나눗셈 연산자는 모두 좌결합, 지수 연산자는 우결합. 예: 2^3^2 = 2^(3^2)이지, (2^3)^2가 아님
수식 1 + 2 * 3 ^ 4 * 5 * 6의 파싱 과정
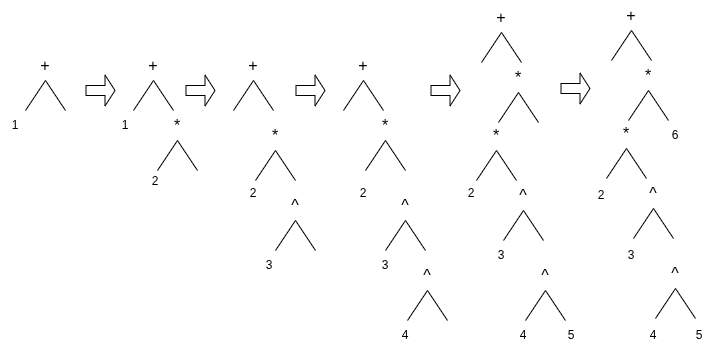
다음 파싱 과정을 통해 괄호없는 수식의 파싱 사고방식을 이해할 수 있다.
수식 파싱 후 최종적으로 얻어지는 파싱 트리는 이진 트리이다. 모든 리프 노드는 피연산자를, 비리프 노드는 연산자를 나타내며 각 연산자는 부모 노드보다 먼저 계산된다. 이는 연산자 우선순위와 결합성을 반영한다.
이 수식 파싱의 기본 사고방식은 왼쪽에서 오른쪽으로 순차적으로 파싱하며 스택을 이용해 이미 읽은 연산자를 기록하는 것이다.
파싱과정은 다음 세가지 상황으로 나눌 수 있다.
- 만약 현재 만난 연산자가 좌결합이고 우선순위가 stack에서 top 연산자의 우선순위보다 높으면
- 해당 연산자를 stack top 연산자의 오른쪽 자식 노드로 만든다.
- 이때 stack top 연산자의 왼쪽 자식 노드는 이미 존재한다.
- 만약 현재 만난 연산자가 좌결합이고 그 우선순위가 stack top 연산자의 우선순위보다 높지 않으면
- 해당 연산자를 stack top 연산자의 부모 노드 또는 조상 노드로 만들어야 한다.
- (stack에서 pop하여 현재 연산자보다 우선순위가 낮은 연산자를 만날때 까지 반복)
- 만약 현재 만난 연산자가 우결합이면 이를 stack top 연산자의 오른쪽 자식 노드로 만든다.
| 우선순위 | 0 | 1 | 2 | 3 | 4 | 6 | 5 | 6 | 5 | 3 | 4 | 0 |
| 수식: | 1 | + | 2 | * | 3 | ^ | 4 | * | 5 | * | 6 | |
| 위치: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Pratt 파싱은 연산자 우선순위와 결합성을 지원하는 파싱 알고리즘이다.
분석의 편의를 위해 이 알고리즘은 각 연산자의 좌우 양쪽에 각각 하나의 우선순위 숫자를 배정하여 연산자의 우선순위를 재현하면서도 결합성을 반영할 수 있게 한다.
좌결합 연산자의 경우, 좌측 우선순위가 우측 우선순위보다 낮다.
우결합 연산자의 경우, 좌측 우선순위가 우측 우선순위보다 높다.
[알고리즘 2: 연산자 우선순위 파싱 알고리즘]
- 입력: 토큰 스트림, 우선순위 (0으로 초기화)
- 출력: 이진 파싱 트리
p[ADD] = (1,2), p[SUB] = (1,2), p[MUL] = (3,4), p[DIV] = (3,4), p[POW] = (6,5);
procedure PRATTPARSE(cur, preced)
let l = cur.next(); // next()는 cur을 다음 위치로 이동하고 해당 위치의 값을 반환
if l.type() ≠ TOK::NUM then
return ERROR;
end if
while true do // 연산자 스택에서 연산자를 팝하는 것에 해당
let op = cur.peek(); // peek()는 다음 위치의 값을 반환
match op.type() :
case TOK::NUM ⇒ exit ERROR;
case TOK::EOF ⇒ return l;
end match
(lp, rp) = p[op];
if lp < preced then
return l;
end if
cur.next();
let r = PrattParse(cur, rp);
let l = CreateBinTree(op, l, r);
end while
return l;
end procedure
알고리즘 2는 Pratt 알고리즘의 의사 코드 구현을 보여준다. 초기 위치의 우선순위를 0으로 가정하고 PrattParse 함수를 호출하면 아까와 같은 구문 분석 트리를 얻을 수 있다.
+
/ \
1 *
/ \
* 6
/ \
* 5
/ \
2 ^
/ \
3 ^
/ \
4 5
[알고리즘 2를 적용하여 수식 1 + 2 * 3 ^ 4 * 5 * 6을 파싱하는 단계]
| cur | preced | l | op | lp | rp | 조작 |
| 0 | 0 | 1 | + | 1 | 2 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 2 | 2 | 2 | * | 3 | 4 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 4 | 4 | 3 | ^ | 6 | 5 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 6 | 6 | 4 | * | 6 | 5 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 8 | 6 | 5 | * | 3 | 4 | return l; |
| 8 | 6 | ^(4,5) | * | 3 | 4 | return l; |
| 8 | 4 | ^(3,^(4,5)) | * | 3 | 4 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 8 | 2 | *(2,^(3,^(4,5))) | * | 3 | 4 | r = PrattParse(cur, rp); l = CreateBinTree(peek, l, r); |
| 10 | 4 | 6 | EOF | - | - | return l; |
| 10 | 2 | ((2,^(3,^(4,5))),6) | EOF | - | - | return l; |
| 10 | 0 | +(1,((2,^(3,^(4,5))),6)) | EOF | - | - | return l; |
해석 실행: 역폴란드 표기법
구문 분석 트리를 기반으로, 후위 순회를 통해 수식의 계산을 완료할 수 있다. 계산기 프로그램의 관점에서 또다른 일반적인 방법은 수식을 역폴란드 표기법(Reverse Polish Notation) 으로 변환하는 것이다.
이는 실제로 구문 분석 트리를 후위순회하여 얻은 토큰 시퀀스이다.
예를 들어 수식 1 + 2 * 3 ^ 4 * 5 * 6의 역폴란드 표기법은 1 2 3 4 5 ^ ^ * 5 * 6 * +이다. (아래 구문 분석 트리를 후위순회)
+
/ \
1 *
/ \
* 6
/ \
* 5
/ \
2 ^
/ \
3 ^
/ \
4 5역폴란드 표기법의 계산은 매우 직관적이다.
순서대로 토큰을 읽어서 피연산자를 만나면 스택에 푸시하고 연산자를 만나면 stack top 의 두 피연산자를 팝하여 계산한후 결과를 다시 stack 에 푸시한다. token읽기가 완료되면 stack top의 원소가 최종 결정된다.
| 단계 | 토큰 | 동작 | stack 상태 |
| 1 | 1 | push | [1] |
| 2 | 2 | push | [1, 2] |
| 3 | 3 | push | [1, 2, 3] |
| 4 | 4 | push | [1, 2, 3, 4] |
| 5 | 5 | push | [1, 2, 3, 4, 5] |
| 6 | ^ | 4^5 = 1024 | [1, 2, 3, 1024] |
| 7 | * | 3*1024 = 3072 | [1, 2, 3072] |
| 8 | * | 2*3072 = 6144 | [1, 6144] |
| 9 | 6 | push | [1, 6144, 6] |
| 10 | * | 6144*6 = 36864 | [1, 36864] |
| 11 | + | 1+36864 = 36865 | [36865] |
결과: 36865
컴파일러 흐름
프로그래밍 언어는 수식보다 복잡하므로 실제 컴파일러는 계산기보다 훨씬 복잡하다.
계산기의 경우 반복문, 조건문, 함수, 변수 등의 기능 없이 오로지 수식 계산만 수행하기 때문에 직접 해석이 가능하다.
반면 일반적인 범용 프로그래밍 언어의 경우 튜링 완전(이론적으로 어떤 계산이든 할수있다.)하므로 이를 사용하여 작성된 프로그램은 범용 튜링 머신에서 실행되어야하며 실제 응용에서는 일반적으로 가상머신과 실제 머신 두가지 방식으로 구현된다.
소스 코드
↓
토큰 스트림
↓
구문 분석 트리
↓
┌─────────────────┼─────────────────┐
↓ ↓ ↓
해석 실행 추상 구문 트리 → 타입 추론/검사
① 계산기 ↓
선형 IR
↓
┌──────────┴──────────┐
↓ ↓
해석 실행 어셈블리 코드
② 가상 머신 ↓
JIT 실행 프로그램
③ 네이티브 실행
References
- Vaughan R. Pratt, "Top down operator precedence."
'System Programming > Compiler' 카테고리의 다른 글
| Compiler 개발 #1 컴파일러 동작 원리 (0) | 2025.12.19 |
|---|---|
| LLVM #1 IR 이해 하기 (0) | 2025.11.11 |
| LLVM #0 LLVM 구조와 동작원리 (0) | 2025.11.10 |